2020. 12. 16. 18:54ㆍComputer Science/AI study

12/16
Lec01: 기본적인 Machine Learning의 용어와 개념 설명
키워드 : 머신러닝, 지도학습, 비지도학습
머신러닝은 일종의 프로그램, 소프트웨어로 explicit programming의 한계(spam filter, automatic driving 의 경우 too many rules)에 대항 가능함. Explicit programming 없이 컴퓨터가 스스로 학습하게 하면 어떨까? 라는 생각에서 출발함.
머신러닝의 학습 방법에는 Supervised learning, Unsupervised learning이 있음
-
Supervised learning 은 labeled training set을 가지고 학습함
Supervised learning을 통해 Email spam filter, Predicting exam score, Image Labeling 문제를 풀 수 있음
-
<Types of supervised learning>
-
regression (predicting final exam score)
-
binary classification (pass/non-pass)
-
multi-label clssification (letter grade A,B,C)
-
Unsupervised learning 은 un-labeled data를 가지고 학습함
Lec02: Simple Linear Regression
키워드 : 선형회귀, 가설, 비용함수
Regression : Regression toward the mean (전체평균으로 돌아감)
Linear Regression : 데이터들을 가장 잘 설명하는 직선의 식(y=ax+b)을 찾는 것 => 즉, a와 b값을 찾는 것

그러면 어떻게 이런 직선을 찾을 수 있을까?
=> Cost 이용! 즉, cost 를 최소로 하는 직선을 찾으면 된다. 아래 사진에서의 H는 가설로서, 예측되는 wx+b 이고 y는 실제 값이다.
이 때, 원래는 Cost가 wx와 y 간의 차이지만, 이 차이는 절댓값이 아니기 때문에 제곱을 하여 cost를 계산함. 따라서, Cost function은 아래와 같이 다시 정의됨.

colab.research.google.com/drive/1v9RhomcG0o5gZXaBXoiut797egR8jYyU?usp=sharing
Google Colaboratory
colab.research.google.com
Lec03: Linear Regression and How to minimize cost
키워드 : 선형회귀, 가설, 비용함수, 경사 하강법, 볼록 함수 (convex function)


이것을 이어 그래프로 그려보면 아래와 같다.

컴퓨터는 경사하강법(Gradient descent algorithm)을 이용해 cost(w)를 최소로 만드는 w 또는 b를 찾아준다.
-
w 와 b 값을 초기화한다. (0,0 또는 any other value)
-
cost(w,b)값을 줄이는 기울기를 선택하여 w와 b를 업데이트한다.
-
w = w - 학습률 * cost(w)의 미분값 (학습률이 클수록 w업데이트가 크게 크게 일어남) (1/2을 곱해준 것은 미분했을 때 더 깔끔하게 식을 표현하기 위함임)

-
반복한다.
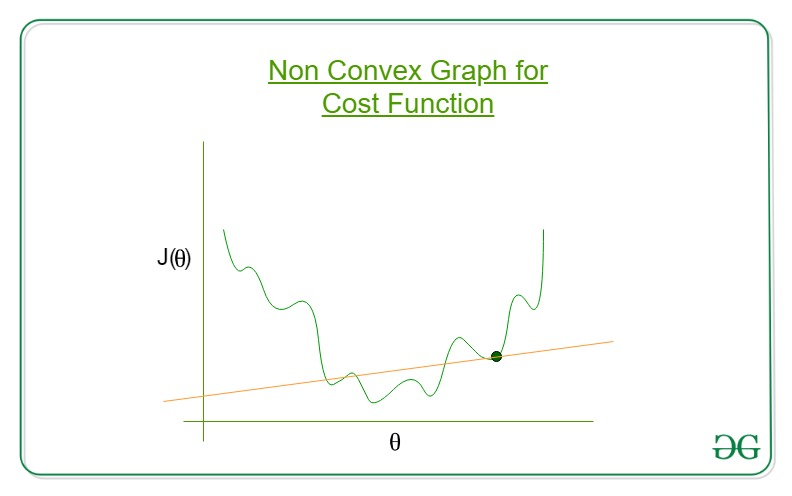
> cost 함수가 볼록함수 (convex function) 인 경우, 초기화 값을 어떤 것으로 해도 최솟값에 도달할 수 있다. 만약, cost 함수가 볼록함수가 아니라면 local minima 문제에 빠지게 되어 경사하강법을 쓸 수 없게 된다.

* cost함수가 convex function이 아닌 경우

colab.research.google.com/drive/1JaARuZ3ANMbu_hlCnGyZANZXRUEKujGA?usp=sharing
Google Colaboratory
colab.research.google.com
Lec04: Multi-variable Linear Regression
키워드 : 다중 선형회귀, 가설, 비용함수, 경사 하강법, 행렬
Multi feature를 이용하여 결과를 예측하는 것이다.
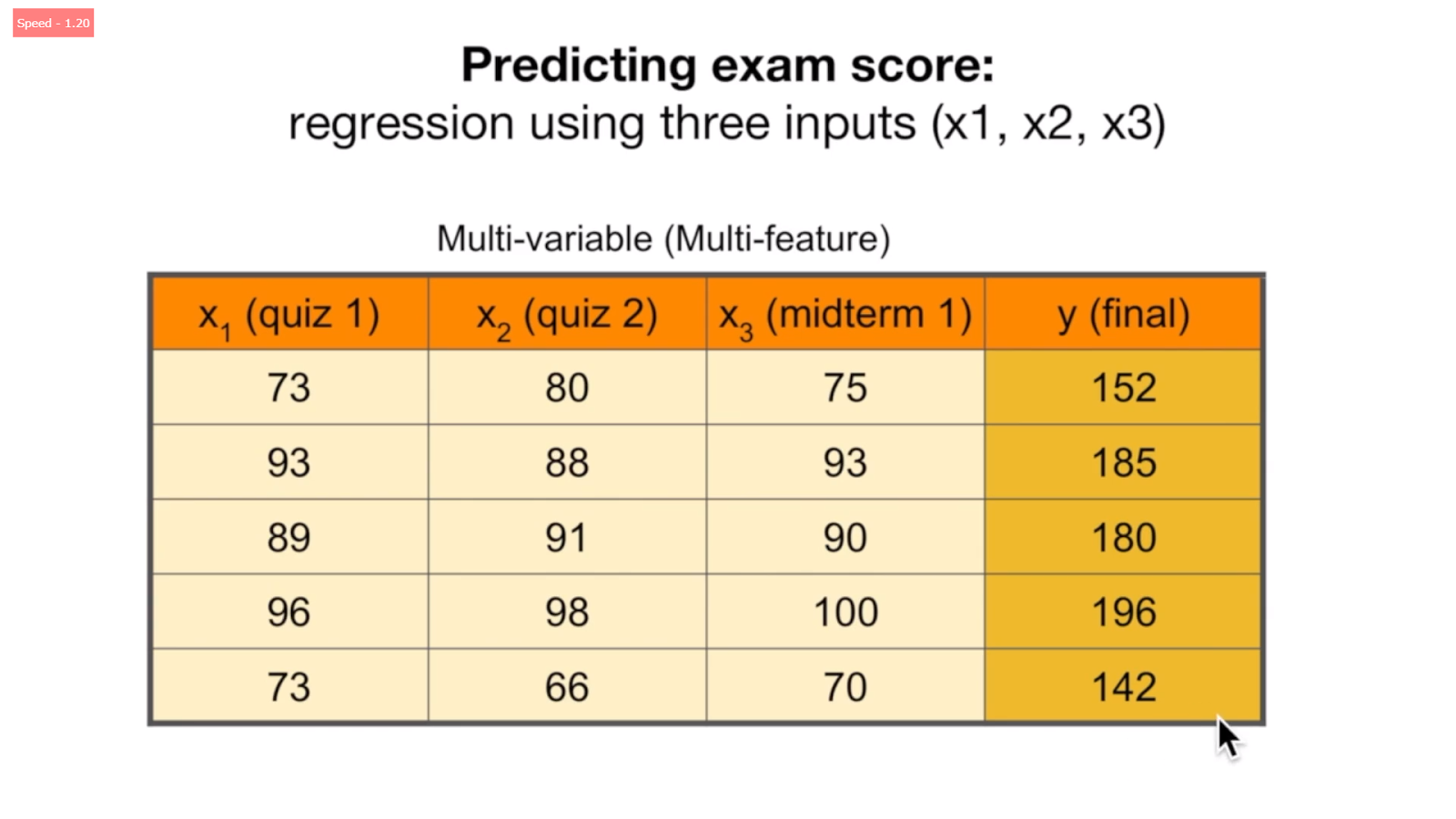
가설함수 H(x1, x2, x3) = w1x1 + w2x2 + w3x3 + b이다. cost 함수는 동일하다. 이 때, feature 수가 많을 수록 곱셈 식을 표현하는 것이 번거로워 매트릭스를 사용하기도 한다.

*여기서 wx가 아니라 xw로 표현하는 것은, 구현 시 학습 데이터가 보통 “행” 형태로 들어오기 때문이다.
매트릭스를 사용하면 feature의 개수나 instance (데이터의 개수, 아래에서는 5개)의 개수에 상관없이 모두 “XW” 라고 표현할 수 있다.

매트릭스를 사용하기 위해서는 데이터의 feature 수와 가중치의 개수가 일치해야 한다.

colab.research.google.com/drive/1papgwnTwJ5SiX3RWoPVtGiXLbPJTKekx?usp=sharing
Google Colaboratory
colab.research.google.com
12/17
Lec05-1: Logistric Regression / Classification
키워드 : 로지스틱 회귀 / 분류, 가설, 시그모이드 / 로지스틱
로지스틱 회귀는 분류 기법 중 하나이다.
Logistic Regression vs Linear Regression

=> Logistic Regression은 Linear Regression 과 달리 분류를 하기 때문에, Output (예측값) 이 0 또는 1 과 같은 형태로 나와야 할 필요가 있다. (ex. 0이면 파란그룹, 1이면 빨간그룹)
Linear Regression의 출력값은 연속형이지만, Logistic Regresion의 출력값은 범주형이다.

=> Logistic Regression는 시그모이드 함수를 사용하여 입력값에 대한 분류를 수행한다. (x값을 가중치, 바이어스와 함께 선형조합하고, 그 선형조합이 시그모이드 함수의 변수로 입력되어 그 output을 이용한 분류가 일어날 수 있게 된다.)
시그모이드 함수의 결과값에 대해서는 0.5를 Desicion Boundary (결정경계)로 하여 분류를 수행한다.
선형회귀에서의 Hypothesis가 Wx+b 였다면, Linear Regression에서의 Hypothesis는 시그모이드 함수의 결과값 (1 / 1+ex) 이다.
Lec05-2: Logistic Regression / Classification의 cost 함수, 최소화
키워드 : 로지스틱 회귀 / 분류, 가설, 시그모이드 / 로지스틱, 비용함수, 최적화
Cost Function for Logistic Regression
=> Logistic Regression에서 선형회귀에서 사용했던 Cost function을 적용해보면 아래와 같은데, 이는 완전한 convex (볼록) 함수도 아닐 뿐더러 분류 상 cost를 올바르게 계산한 것이라 볼 수 없다. (EX. 정답이 1인 것에 대해 1로 분류한 경우는 cost가 0, 0으로 분류한 경우는 cost가 1이어야 함)
따라서, Logistic Regression에서 사용하는 cost function은 다음과 같다.


(Logistic Regression은 출력값이 범주형인 분류용 함수이기 때문에, h(x)의 값으로 나오게 되는 것은 0또는 1 뿐이고, 따라서 위의 Cost 함수의 결과값으로 나오는 것도 각각 2가지, 총 4가지 뿐이다.)
위의 Cost 함수를 하나의 식으로 표현하자면,
Cost = -y log (h(x)) - (1-y) log (1-h(x)) 이다.
그럼 Logistic Regression 에서 cost 값을 최소화 (optimization) 하는 방법은 무엇일까?
=> 똑같이 경사하강법을 사용하면 된다. (위에서 만든 log 기반 cost함수는 삐뚤빼뚤하지 않은 convex 모양이기 때문에)
colab.research.google.com/drive/1rIb2SKd3mO8L_FCcMW0P65I3HOANWKvS?usp=sharing
Google Colaboratory
colab.research.google.com
Lec06-1: Softmax Regression 기본 개념소개
키워드 : 다항 분류 (Multinomial Classification)
앞서 배웠던 이항 분류 (Binary Classification)를 응용하여 다항분류를 수행할 수 있다.
즉, A와 not A / B와 not B / C와 not C로 구분하도록 이항분류를 3개 만들 수 있다.

이를 매트릭스로 표현하면 아래와 같다. (현재는 매트릭스의 출력값이 연속형 범주에 속하는 어떠한 수들임. (not 확률) 그러나 결론부터 말하자면, 이러한 매트릭스의 출력값에 시그모이드를 적용하여 각 범주에 속할 확률로 변환함)

=> 그렇다면 시그모이드는 어디서 어떻게 사용되는 걸까?
: 다음 장에서 학습
colab.research.google.com/drive/1OZJmcL91Hm4Z7UcKsWrhGUKMTtPySR_S?usp=sharing
Google Colaboratory
colab.research.google.com
Lec06-2: Softmax Classifier의 cost 함수
키워드 : 다항 분류 (Multinomial Classification), 소프트맥스, 크로스 엔트로피, 경사하강법
위의 WX 값을 0과 1사이의 확률로 바꾸기 위해서 softmax 함수를 사용한다. (이항분류에서 가설함수를 만들 때 선형조합을 시그모이드 함수에 대입했던 것처럼, 다항분류에서 가설함수를 만들 때에는 선형조합을 소프트맥스 함수에 대입한다. )
이 때, Softmax 함수를 사용함으로써 확률의 총 합을 1로 만들 수 있어 범주 간 확률을 비교하기 좋다.


위와 같이 원핫 인코딩(one-hot encoding)으로 범주를 표현할 수도 있다.
그럼 다항분류에서 사용하는 cost function은 무엇일까?
=> 바로 교차 엔트로피이다. (S는 예측값, L은 실제값)

교차엔트로피가 정말 적절한 다항분류의 코스트함수가 될 수 있는지 보기 위해서 아래와 같은 예시를 들어보자. 실제 범주가 B인 것을 B로 예측했을 때의 cost는 0인 것을 알 수 있다.

여러 개의 입력데이터에 대해서는 아래와 같이 일반화하여 (평균구하기) 코스트를 구할 수 있다.

다항분류의 cost 함수에 대한 최솟값은 역시 경사하강법을 사용하여 구할 수 있다. (cost 함수가 convex 모양이므로)
colab.research.google.com/drive/1z47Bi8Omzza-tP_XhYNxMczsxByg6-MV?usp=sharing
Google Colaboratory
colab.research.google.com
12/19
Lec07-1,07-2: Application & Tips : 학습률과 데이터전처리
키워드 : 학습률 (learning rate), 데이터전처리
-
학습률은 어떻게 조정할까?
학습률은 Hyper-parameter로, 손실함수의 기울기를 얼마만큼 고려하여 weight를 조정하는지에 관여한다. 즉, 경사하강법에서 한번에 가로방향으로 얼만큼 이동하는지를 의미함.

보통 학습률로는 0.01을 많이 쓴다.
또한, 학습과정에서 learning rate를 조정해나가는 것을 Annealing 이라고 함
=> 학습 과정에서 일정 epoch에 도달하면 더 이상 학습이 일어나지 않아, cost의 변화가 일어나지 않는 지점이 있는데, 이 때 learning rate를 조절하여 cost값을 계속 최소화 해 나갈 수 있다.

> Annealing 방법에는 아래의 것들이 있다.
step decay(일정 epoch 마다 일정 step 만큼 learning rate를 조정),
exponential decay(일정 epoch 마다 exponential 을 이용하여 learning rate를 조정),
1/t decay
> 이러한 다양한 Annealing 기법은 tensorflow에서 제공하고 있음
2. 데이터 전처리의 기법들에는 무엇이 있을까?
ㄱ. Feature Scaling
: 여러 가지의 데이터가 입력되는 경우, 데이터마다의 unit 등이 다르다는 것이 데이터의 최종영향력에 영향을 미칠 수 있다. 이것을 대비하여, 데이터끼리의 unit 등, 범위를 대략 맞춰준다. (ex. 키와 몸무게가 입력데이터로 들어왔을 때, 키는 보통 몸무게보다 숫자가 크므로 키 데이터가 몸무게 데이터보다 더 영향력을 크게 미칠 수 있다. 이 경우, 키와 몸무게 데이터의 unit 이 달라 발생하는 문제로 두 데이터에 적절한 전처리를 수행해야 한다.)
=> Min-Max Normalization (최소, 최댓값을 알 때 사용 / 데이터를 일반적으로 0~1 사이의 값으로 변환시켜준다.)
Normalization => x_new = (x - x_min) / (x_max - x_min)
=> Standardization (최소, 최댓값을 모를 때 사용 / 기존 변수의 범위를 정규분포로 변환하다.)
ㄴ. Noisy data 없애기
3. 과적합은 무엇이고, 해결방안은 무엇일까?

테스트데이터와 검증데이터 모두에 대해 높은 정확도를 보여야 좋음
Solution for overfitting =>
학습데이터 양을 늘리기(ex. 이미지에서는 color jilttering, horizontal flips 등의 기법이 있다.), Feature의 수를 줄이기(with PCA 방법으로), 추가적으로 feature의 수를 늘리기, 정규화하기 (Regularization이라고도 하며, with Add term to loss 방법으로), Drop out, Batch Normalization 등
특히, 이 중 정규화하기 방법은 손실함수에 추가적으로 가중치 제곱들의 평균값을 더함으로써 시킬 수 있다고 한다.

> 세타 2 (가중치)의 값이 100으로 다른 가중치들에 비해 유독 큰 경우를 생각해보자. 이 경우, 세타 2 가중치의 영향력이 다른 가중치에 비해 매우 커지게 되고, 이는 과적합을 유발할 수 있다. 따라서, cost 함수를 생성할 때 가중치 제곱 합의 평균을 추가적으로 고려하여 과적합을 피할 수 있다고 한다.
colab.research.google.com/drive/1Evsip0JAvPE0zYxKDg-9ksMGKrU_yaUY?usp=sharing
Google Colaboratory
colab.research.google.com
Lec07-3: Application & Tips : Data & Learning
키워드 : 데이터세트(data set): 훈련(training), 평가(validation), 테스트(test) 데이터, 온라인학습, 배치학습, 파인튜닝(fine tuning)
- 데이터 세트 : 데이터를 학습, 평가 데이터로 나눌 때 적절하게 나누는 것이 매우 중요하다.
- 학습방법에는 온라인학습(online learning)과 배치학습(offline learning)이 있다.

이 외에도 Fine Tuning, Feature Extraction 과 같은 학습 방법도 있다.
Fine Tuning : 새로운 데이터로 다시 한 번 weight 값을 미세하게 조정해서 새로운 데이터에 대해서도 학습을 잘 할 수 있도록 하는 것, 기존에 학습되어져 있는 모델을 기반으로 아키텍쳐를 새로운 목적에 맞게 변형하고, 이미 학습된 모델 weights로부터 학습을 업데이트 하는 방법
Feature Extraction : 기존 모델과 가중치는 그대로 두고, 새로운 레이어를 추가해서 이를 학습시켜 새로운 데이터에 대한 학습을 잘 할 수 있도록 하는 것

=> 최근에는 모델의 속도를 빠르게 하기 위해서 weight를 경량화하는 방향으로 딥러닝이 발전되고 있음 (ex. cnn)
colab.research.google.com/drive/1KhOTY8aeonakFpZ7Gq6gbiBKaLRng6nG?usp=sharing
Google Colaboratory
colab.research.google.com